模式识别(Pattern Recognition)学习笔记
Pattern Recognition EM HMM
1 期望最大法EM
EM算法,全称 Expectation Maximization Algorithm。期望最大算法是一种迭代算法,用于含有隐变量(Hidden Variable)的概率参数模型的最大似然估计或极大后验概率估计。
从定义可知,该算法是用来估计参数的,这里约定参数为$\theta$。既然是迭代算法,那么肯定有一个初始值,记为$\theta_{(0)}$,然后再通过算法计算$\theta_{(1)},\theta_{(2)},…,\theta_{(t)}$。
通常,当模型的变量都是观测变量时,可以直接通过极大似然估计法,或者贝叶斯估计法估计模型参数。但是当模型包含隐变量时,就不能简单的使用这些估计方法
1.1 思想
EM 算法的核心思想非常简单,分为两步:Expection-Step 和 Maximization-Step。E-Step 主要通过观察数据和现有模型来估计参数,然后用这个估计的参数值来计算似然函数的期望值;而 M-Step 是寻找似然函数最大化时对应的参数。由于算法会保证在每次迭代之后似然函数都会增加,所以函数最终会收敛。
1.2 举例
参考【机器学习】EM——期望最大(非常详细) 2.1例子A和2.2例子B 以及 怎么通俗易懂地解释EM算法并且举个例子?
1.3 推导
举个具体的栗子:K-means算法中,除了给定的样本(也就是观测变量)$X$以及参数$\theta$(也就是那些个聚类的中心)之外,还包含一个隐变量(记为$Z$),它是每个样本的所属类别
可以理解为,我们之所以对一批样本进行聚类,也是因为认为这些样本是有它们潜在的类别的,也就是说还有一个隐变量是我们没有(或者无法)观测到的
下面先给出EM算法的步骤公式,然后再对公式进行推导。假设在第$i$次迭代后参数的估计值为$\theta_{(i)}$,对于第$i+1$次迭代,分为两步:
- E-step, 求期望(对缺失数据):
- M-step,最大化:
其中,$Q(\theta,\theta_{(i)})$称为$Q$函数,是EM算法的核心。公式推导见EM算法原理及推导和EM算法-数学原理及其证明
1.4 算法流程
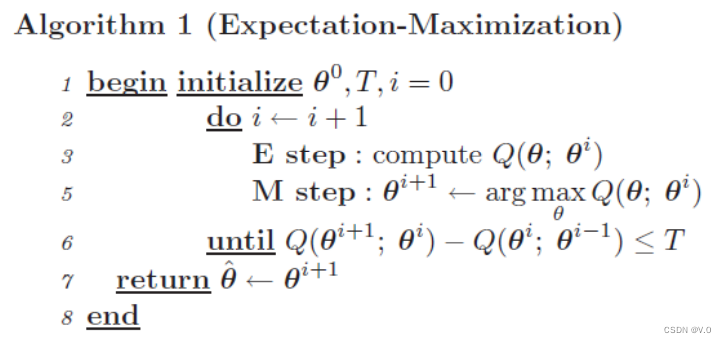
图1 EM算法流程
2 隐马尔科夫模型HMM
2.1 马尔可夫模型
概念
在某段时间内,交通信号灯的颜色变化序列是:红色 - 黄色 - 绿色 - 红色。
在某个星期天气的变化状态序列:晴朗 - 多云 - 雨天。
像交通信号灯一样,某一个状态只由前一个状态决定,这就是一个一阶马尔可夫模型。而像天气这样,天气状态间的转移仅依赖于前 n 天天气的状态,即状态间的转移仅依赖于前 n 个状态的过程。这个过程就称为n 阶马尔科夫模型。
不通俗的讲,马尔可夫模型(Markovmodel)描述了一类重要的随机过程,随机过程又称随机函数,是随时间而随机变化的过程。
定义及假设
存在一类重要的随机过程:如果一个系统有N个状态$S1,S2,…,S_N$。随着时间的推移,该系统从某一状态转移到另一状态。如果用$q_t$表示系统在时间t的状态变量,那么t时刻的状态取值为$S_j$(1<=j<=N)的概率取决于前t-1个时刻(1, 2, …, t-1)的状态,该概率为:
\[p(q_t=S_j|q_{t-1}=S_i,q_{t-1}=S_k,...)\]假设一:如果在特定情况下,系统在时间t的状态只与其在时间t-1的状态相关,则该系统构成一个离散的一阶马尔可夫链:
\[p(q_t=S_j|q_{t-1}=S_i,q_{t-1}=S_k,...)=p(q_t=S_j|q_{t-1}=S_i)\]假设二:如果只考虑独立于时间t的随机过程,状态与时间无关,那么$p(q_t=S_j|q_{t-1}=S_i)=a_{ij},1<=i,j<=N$,即:t时刻状态的概率取决于前t-1个时刻(1, 2, …, t-1)的状态,且状态的转换与时间无关,则该随机过程就是马尔可夫模型。
2.2 隐马尔可夫模型
概念
在马尔可夫模型中,每个状态代表了一个可观察的事件,所以,马尔可夫模型有时又称作可视马尔可夫模型(visibleMarkovmodel,VMM),这在某种程度上限制了模型的适应性。对于盲人来说也许不能够直接获取到天气的观察情况,但是他可以通过触摸树叶通过树叶的干燥程度判断天气的状态。于是天气就是一个隐藏的状态,树叶的干燥程度是一个可观察的状态,于是我们就有了两组状态,一个是不可观察、隐藏的状态(天气),一个是可观察的状态(树叶),我们希望设计一种算法,在不能够直接观察天气的情况下,通过树叶和马尔可夫假设来预测天气。
以一个一阶的隐马尔可夫模型为例,在隐马尔可夫模型(HMM)中,我们不知道模型具体的状态序列,只知道状态转移的概率,即模型的状态转换过程是不可观察的。因此,该模型是一个双重随机过程,包括模型的状态转换和特定状态下可观察事件的随机。
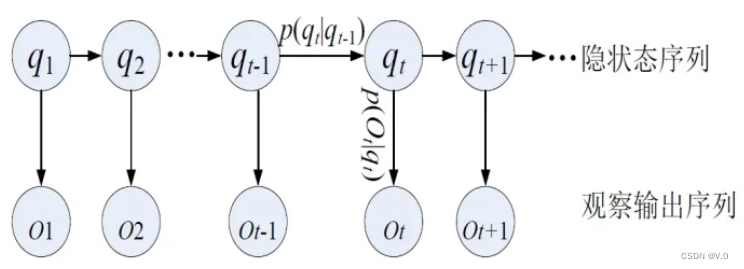
图2 一阶HMM
HMM组成
例如,N 个袋子,每个袋子中有 M 种不同颜色的球。选择一个袋子,取出一个球,得到球的颜色。
1、状态数为 N(袋子的数量)
2、每个状态可能的符号数 M(不同颜色球的数目)
3、状态转移概率矩阵 $A=a_{ij}$(从一只袋子(状态$S_i$) 转向另一只袋子(状态$S_j$) 取球的概率)
4、从状态$S_j$观察到某一特定符号$v_k$的概率分布矩阵为:$B=b_j(k)$(从第 j 个袋子中取出第 k 种颜色的球的概率)
5、初始状态的概率分布为:$\pi=\pi_i$
一般将一个隐马尔可夫模型记为:$\lambda=[\pi,A,B]$
需要确定以下三方面内容(三要素):
1、初始状态概率$\pi$: 模型在初始时刻各状态出现的概率,通常记为$\pi=(\pi_1,…,\pi_N)$,$\pi_i$表示模型的初始状态为$S_i$的概率.
2、状态转移概率A: 模型在各个状态间转换的概率,通常记为矩阵$A[a_{ij}]$,其中$a_{ij}$表示在任意时刻 t,若状态为$S_i$,则在下一时刻状态为$S_j$的概率.
3、输出观测概率B: 模型根据当前状态获得各个观测值的概率通常记为矩阵$B=[(b_{ij})]$。其中,$b_{ij}$表示在任意时刻t,若状态为$S_i$,则观测值$O_j$被获取的概率.
相对于马尔可夫模型,隐马尔可夫只是多了一个各状态的观测概率。给定隐马尔可夫模型$\lambda=[A,B,\pi]$,它按如下过程产生观测序列{$X_1,X_2,…,X_n$}:
(1) 设置t=1,并根据初始状态概率$\pi$选择初始状态$Y_1$;
(2) 根据状态值和输出观测概率B选择观测变量取值$X_t$;
(3) 根据状态值和状态转移矩阵A转移模型状态,即确定$Y_{t+1}$;
三个问题
一旦一个系统可以作为 HMM 被描述,就可以用来解决三个基本问题。
1、 评估(Evaluation)
给定 HMM,即$\mu=[\pi,A,B]$,求某个观察序列的概率。 例如:给定一个天气的隐马尔可夫模型,包括第一天的天气概率分布,天气转移概率矩阵,特定天气下树叶的湿度概率分布。求第一天湿度为 1,第二天湿度为 2,第三天湿度为 3 的概率。
2、 解码( Decoding)
给定 HMM,即$\mu=[\pi,A,B]$,以及某个观察序列,求得天气的序列。 例如:给定一个天气的隐马尔可夫模型,包括第一天的天气概率分布,天气转移概率矩阵,特定天气下树叶的湿度概率分布。并且已知第一天湿度为 1,第二天湿度为 2,第三天湿度为 3。求得这三天的天气情况。 即:发现“最优”状态序列能够“最好地解释”观察序列
3、 学习(Learning)
给定一个观察序列,得到一个隐马尔可夫模型。 例如:已知第一天湿度为 1,第二天湿度为 2,第三天湿度为 3。求得一个天气的隐马尔可夫模型,包括第一天的天气,天气转移概率矩阵,特定天气下树叶的湿度概率分布。